摘要

利用几何不变量理论，研究了平面性学中铅笔的射影等价分类问题。特别地，我们完整地描述了由G. Halphen于1882年首次提出的平面性铅笔(称为指数双经典几何对象的Halphen铅笔)的GIT稳定性。受Miranda关于平面立方体铅笔的工作的启发，我们根据出现在其相关有理椭圆表面上的奇异纤维的类型获得了明确的稳定性标准。

1 介绍

分类问题通常是通过代数群的作用构造商空间来解决的，而几何不变理论(GIT)为构造这种商提供了一个工具。本文主要研究平面性的铅笔分类问题，以达到射影等价。

设V为截面空间，则d次平面曲线的铅笔空间可以用直线的格拉斯曼坐标来标识，并通过plpl cker坐标嵌入其中。群SL(V)Footnote 1自然作用于V，因此作用于不变子变量，一个经典问题是构造相应的GIT商。这相当于确定这个动作的(半)稳定铅笔是什么。

在[1]中，我们将铅笔在SL(V)作用下的GIT稳定性与对数正则阈值联系起来，其中是曲线In(参见示例[2,section . 8]);也与一个基点上的生成器的多重性有关。结果在[1]然而，只提供(半)稳定铅笔的部分描述。

在第2节中，我们根据铅笔的pl cker坐标上的一些消失条件获得了明确的稳定性判据，从而完成了描述。这就是命题2.2和命题2.3的内容。在第3节中，我们将重点放在平面性的特定铅笔上，并从几何上解释这种消失标准。

在第四节中，我们将注意力转向指数二的所谓哈尔芬铅笔，以法国数学家乔治·亨利·哈尔芬(Georges Henri Halphen)的名字命名，他在[3]中首次研究了这种铅笔。我们提供了一个完整的和几何的描述，他们的稳定性视为点在。受[4]的启发，我们根据出现在其相关有理椭圆表面上的奇异纤维类型获得了明确的稳定性判据。相关定义如下:

定义1.1

指数为二的哈芬铅笔是由六次平面曲线组成的铅笔，它有九个(可能无限接近)倍数为二的基点。

定义1.2

有理椭圆曲面由光滑的、射影的有理曲面Y和一条纤维组成，使得一般纤维是光滑的属1曲线，任何纤维中都没有-曲线。我们将纤维的指数定义为理想的正发生器，其中表示一般纤维。

此外，Halphen铅笔与有理椭圆曲面的对应关系由以下命题给出:

命题1.3

[5，定理5.6.1]]如果是指标2的有理椭圆曲面，则存在一个双分形映射，它是指标2的Halphen铅笔。反之，给定指标2的Halphen铅笔，取其基点的最小分辨率，得到指标2的有理椭圆曲面。

Y表面有有限多个奇异纤维，所有非多重奇异纤维的构型与相关雅可比纤维中的构型完全相同(参见[6，第V.9章])。特别是，可能的纤维类型已经被Kodaira和nsamron分类[7,8,9]。此外，Miranda和Persson[10,11]还对奇异纤维的可能构型进行了分类。并且，在特征为零的场上，任何多重光纤都是某些类型的[5，命题5.1.8]。

本文的主要结果由下面的定理1.4、1.5和1.6给出，其中表示指标2的Halphen铅笔，Y表示相应的有理椭圆曲面。我们写为，其中C是通过的九个基点的唯一三次曲线B对应于Y的某个(非多重)纤维，我们用F表示。

我们的方法的主要思想之一是观察群SL(V)也作用于平面性空间。在[1]中，我们还将铅笔的稳定性与其发电机的稳定性联系起来，并且六次平面曲线的稳定性是众所周知的- Shah在[12]中已经完全描述了它。

其他主要成分是:(1)[13]中索引2的Halphen铅笔的明确构造和其中的定理1.2的分类，(2)由[13，定理1.1]提供的不等式，(3)在[1]中给出的稳定性判据，以及(4)第3节的结果。

利用椭圆曲面奇异纤维的Kodaira符号，考虑到SL(V)对椭圆曲面奇异纤维和六次平面曲线空间的作用，证明:

定理1.4

当C是光滑的，铅笔是稳定的当且仅当下列陈述之一成立

1. (i)

   Y的所有纤维都被还原

2. (2)

   Y只包含一个(非多个)类型为或的纤维F

3. (3)

   Y只包含一根(非多根)或型光纤F，且对应的平面曲线B为半稳定曲线

4. (iv)

   Y包含两种类型的纤维，并且不存在同时破坏两条相应曲线的单参数子群。

定理1.5

当C是单数时，铅笔是稳定的当且仅当下列陈述之一成立

1. (i)

   Y的所有纤维都被还原

2. (2)

   Y包含一个(非多重)非还原纤维F，使得对应的曲线B是半稳定的;没有一个单参数子群能同时破坏2C和B的稳定

3. (3)

   Y中含有类型为光纤的光纤，B中含有不稳定光纤

定理1.6

铅笔是半稳定的当且仅当每条曲线都是半稳定的或Y不包含类型为F的纤维。

我们从头到尾都在加班。

2 平面性铅笔的稳定性

描述GIT意义上的稳定性的一个基本工具是Hilbert-Mumford的数值准则。在我们的设置中，它说铅笔是不稳定的。非稳定)，当且仅当存在一个1参数子群，其所有权值都是正的。非负)。特别是，为了确定哪些是(半)稳定铅笔，我们需要知道SL(V)中的对角线元素如何作用于pl cker坐标。

如果我们选择一支铅笔和两条曲线作为生成器，它们分别用和表示(在某种坐标选择中);那么plencerker嵌入将矩阵带至其坐标由所有子矩阵给出的点。

现在，如果SL(V)中的一个元素是由坐标系[x, y, z]中的某个选择给出的，那么它对坐标系的作用是由。因此，作用于一个点的作用是由给出的，因此，它作用于plicker坐标是由

因此，我们可以将铅笔稳定性的希尔伯特-芒福德判据表示为它的一些plicker坐标的消失(相对于基的方便选择)。

首先，请注意，我们可以假设SL(V)的任何单参数子群是归一化的，这意味着我们选择坐标[x, y, z]，使其由

哪里和哪里。

特别地，在pl克尔坐标系中的作用由

在哪里。

此外，我们可以对权重进行标准化，这样对于一些。然后

Hilbert-Mumford权值(定义见下文(1))的符号在这些简化下没有改变，Hilbert-Mumford准则变成:

命题2.1

铅笔是不稳定的。(非稳定)当且仅当存在有理数和有理数中的坐标，当铅笔在这些坐标中表示为，则无论何时(请参考)．

先验地，对于每一个坐标的选择，都需要测试所有可能的值来验证稳定性判据。然而，因为函数(对于一个固定的和一些选择的坐标)

（1)

是分段线性的，一个关键的观察是，我们只需要对有限数量的临界值检验它的正性。

换句话说，条件(p.)将该区间划分为有限多个子区间，在这些子区间内不等式的真性保持不变。也就是说，对于每个区间，我们可以找到i, j, k和l的值，对于这些值，不等式(resp。)对所有人都适用。

为了找到这些间隔，我们按如下步骤进行。由于计算的原因，我们首先让和。然后，对于集合中每个可能的对(r, s)

我们检验是否能解出不等式。对于变量a，进一步施加限制。

存在可能的对(r, s)，我们找到的a对应的值可以总结如下表1和表2所示。

然而，在这一点上，pl cker坐标上相应的消失条件不是独立的。但是，仔细检查表1和表2，就会发现给出不稳定性最小条件的子区间的数量(参见表2)。不稳定性)实际上是6(参见。7)。

更确切地说，为了得到不稳定的最小条件，只考虑以下六个不同的子区间就足够了:

同样地，对于非稳定性，取

因此，通过对表1和表2中的数据进行分析，我们得出了不稳定性的Hilbert-Mumford判据(见第2章)。非稳定性)可在提案2.2(见第2章)中重新表述。(命题2.3)，其中我们将介绍以下几组:

和

命题2.2

铅笔是不稳定的，当且仅当存在坐标，所以如果铅笔在这些坐标中表示为，那么

情况下 U(1):

in对于所有对(r, s)都消失，并且表现为不稳定;或

情况下 U(2):

in对于所有对(r, s)都消失，并且表现为不稳定;或

情况下 U(3):

in对于所有对(r, s)都消失，并且表现为不稳定;或

情况下 U(4):

in对于所有对(r, s)都消失，并且表现为不稳定;或

情况下 U(5):

in对于所有对(r, s)都消失，并且表现为不稳定;或

情况下 U(6):

in对于所有对(r, s)都消失，并且表现为不稳定。

命题2.3

铅笔是不稳定的当且仅当存在坐标系所以如果铅笔在坐标系中被表示为，那么

情况下 NS(1):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(2):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(3):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(4):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(5):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(6):

对于和中的所有对(r, s)， in都消失，表现为不稳定;或

情况下 NS(7):

in对于所有对(r, s)都消失，并且表现为不稳定。

话2.4

注意，如果铅笔满足命题2.2中情形U(i)的消失条件，则它满足命题2.3中情形U(i)的消失条件。

3.不稳定和不稳定铅笔

给定一个不稳定的响应。非稳定的)铅笔，如果我们选择坐标[x, y, z]在命题2.2(见第2页)。2.3)和发电机和，则每个消失条件可以转化为某些对和发电机的系数消失(不一定是原始对)。然后，我们可以通过在平面上的系数三角形中表示(和)来可视化稳定性判据，如[14，第1.9节]所示。

例如，如果我们假设满足情形NS(1)的条件。那么，在图1中的一种情况(见第2页)中，定义多项式和的系数位于相应线的下方。2)必须全部消失。

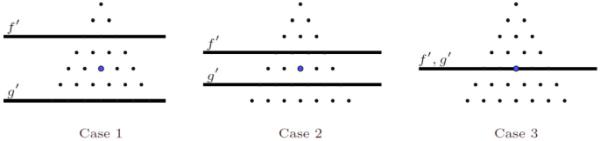
命题2.3的情形NS(1)的图象描述

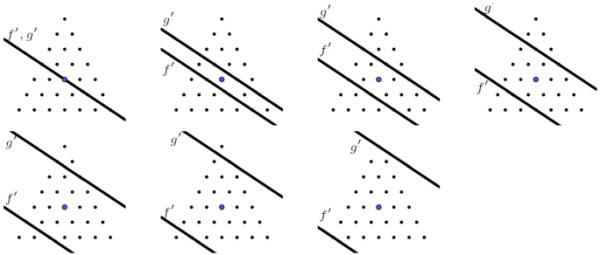
命题2.3的情形NS(4)的图象描述

我们可以为命题2.2和2.3中的每一种情况画出类似的图，从而用它们的产生器的显式方程得到不稳定铅笔和不稳定铅笔的特征。

为了说明在这个过程中涉及到什么样的计算，我们在下面证明命题3.1，它对应于图1。我们用这个符号表示由单项式生成的变量x、y和z的六次齐次多项式的子空间。而表示由所有不同于的单项式生成的多项式的子空间。结果如下:

命题3.1

铅笔满足命题2.3情形NS(1)中的消失条件，当且仅当和产生器中存在坐标，并且满足

情况下1：

g是任意的

情况下2：

和

情况下3：

F和，其中和

证明

让我们假设它是不稳定的，并且对于所有满足命题2.3的情形NS(1)中的i, j, k和l以及所有对(r, s)，它的plicker坐标必须消失。使用关系和我们可以计算最小值集(按顺序)，以便消失。

换句话说，我们找到所有符合限制条件的整数i j k l

1. (i)

   ，

2. (2)

   ，

3. (3)

   ,

4. (iv)

满足不等式

所有可能的解决方案(按顺序)如下:

接下来的问题是如何确定在定义多项式的生成器中哪些系数需要消失。

注意，我们已经引入了pl 克尔坐标的排序，来自于对i, j, k和l的限制，所以，第一步是看上面列表中第一项的方程，也就是我们看这个方程。因此，要么

1. （1)

   或

2. (2）

   或

3. （3）

此外，如果(2)(或(3)由对称)成立，那么我们可以假设并且我们必须有。

接下来，对于上面的每一种情况，看看下一个消失条件来自于列表的第二项。同样，有三种可能性:非此即彼。

我们以这种方式进行，直到没有更多的方程需要解为止。

事实上，我们的列表告诉我们，消失为所有(适当的)和。因此，我们的算法告诉我们，如果我们处于情形(2)的情况下，那么对于所有kl，其中一个生成器属于。而且，根据对称性，如果(3)成立，我们得到同样的结论。类似的推理适用于下一组消失条件，以此类推。

然而，重要的是要注意，在求解方程的每一步中，我们都必须考虑系数和是否有先前的条件。

通过遵循草图算法，我们得到了铅笔所需的描述。

特别是,

3.1.1必然

如果包含如下形式的曲线，其中L为直线，Q为二次曲线，则是非稳定的。

现在，在命题3.1的证明中所采用的同样的算法，可以更普遍地应用于任何不稳定的情况。非稳定)，并满足命题2.2(见第2章)中的一种情形中的消失条件之一。2.3)。然而，所涉及的计算非常冗长，完整的描述可以在[15]中找到。我们在这里只提出对第4节索引2的Halphen铅笔的研究至关重要的结果。我们关注的是包含有多条线作为组成部分的曲线的铅笔，这是合适的。

定义3.2

如果铅笔上的任意两条曲线正确相交，即它的基底轨迹是零维的，那么它就是固有的。

我们证明的第一个结果如下:

命题3.3

如果我们能在和的生成器中找到坐标，并且使得和g是任意的，那么铅笔将满足命题2.2的情形U(1)中的消失条件。特别是，如果含有曲线的形式，其中L和为直线，则是不稳定的。

证明

事实上，所有plencker坐标都消失了，除了(可能):和。请注意。

我们还证明:

命题3.4

设一个合适的铅笔，它包含如下形式的曲线，其中L是一条直线，Q是一条圆锥曲线(可能可约)。如果是不稳定的，那么存在这样的坐标系和另一个生成器

1. (i)

   L与[0,0,1]相切，具有多重性;或

2. (2)

   L与[0,0,1]相切，多重度为4，而[0,0,1]的多重度为;或

3. (3)

   L与[0,0,1]相切，多重性为和。

证明

我们首先注意到，根据推论3.1.1，总是不稳定的。事实上，满足命题2.3的情形NS(1)中的消失条件(或者等价地，满足命题3.1的情形1)。现在，利用命题3.1的证明中所描述的算法，我们可以证明，如果是不稳定的，则存在坐标系和另一个这样的生成器:

1. (i)

   和

2. (2)

   或

3. (3)

   和

4. (iv)

   或

5. (v)

   和

此外，与命题3.4的证明相同的推理也表明:

命题3.5

设一个合适的铅笔，它包含如下形式的曲线，其中L是一条直线，C是一个三次(可能可约)。如果是不稳定的，那么存在这样的坐标系和另一个发生器

和:

1. (i)

   L与[0,0,1]相切，其多重性为6，而[0,0,1]的多重性为;或

2. (2)

   L与[0,0,1]相切，多重度为5，[0,0,1]在和中具有多重度L与C在[0,0,1]处的交多重度为1;或

3. (3)

   L与[0,0,1]相切，多重度为5，[0,0,1]的多重度为，L与C在[0,0,1]处的交多重度为;或

4. (iv)

   L与[0,0,1]相切，多重度为4，[0,0,1]的多重度为，L与C在[0,0,1]处的交多重度为2;或

5. (v)

   L与[0,0,1]相切，具有多重性，L与C在[0,0,1]的交多重性为3。

命题3.6

设一个合适的铅笔，它包含如下形式的曲线，其中L是一条直线，Q是一个四次(可能可约)。如果是不稳定的，那么在和的产生器中存在这样的坐标:

对于某些值，L的正切次数为6，而[0,0,1]的乘法次数为。

命题3.7

设一个合适的铅笔，它包含如下形式的曲线，其中L是一条直线，C是一个三次(可能可约)。如果是非稳定的，则在和另一个生成器中存在坐标，使得和:

1. (i)

   L与[0,0,1]相切，多重度为6

2. (2)

   L与[0,0,1]相切，多重度为5，而[0,0,1]的多重度为

3. (3)

   L与[0,0,1]相切，多重度为4，而[0,0,1]的多重度为

4. (iv)

   L与[0,0,1]相切，多重度为4,L与C在[0,0,1]处的交多重度为

5. (v)

   L与[0,0,1]相切，具有多重性，[0,0,1]具有多重性，且L与C在[0,0,1]处的交多重性为2

6. (vi)

   L和(p.)的交多重性。C)在[0,0,1]处是(resp.)。3)。

4 指数二的半铅笔的稳定性

最后，我们可以证明定理1.4、1.5和1.6了。这就是本节的目标。受[4]的启发，我们将根据相应的有理椭圆表面上出现的奇异纤维类型(见定义1.2和命题1.3)，对指数2的Halphen铅笔(定义1.1)的稳定性进行完整的几何描述。

我们的策略可以概括如下:将我们在[1]中得到的稳定性判据与[13,16,17]的结果(下面的引理4.1,4.3和4.4)结合起来，我们可以首先给出(半)稳定的一些充分条件。这是在4.1节中实现的。然后，通过进一步研究Y中含有或型纤维F的情况(第4.2、4.3和4.4节)，可以得到完整的稳定性表征。对于这些最后的步骤，我们使用第3节的结果和[13，第7节]的明确结构。

请注意，它恰好包含一个多重立方2C，对应于Y中的唯一多重光纤[5，命题5.61，(iii)]。因此，可以写成下面的形式，其中曲线B对应于我们用f表示的Y的某个(非多重)纤维。我们将自始至终使用这些符号。

4.1 足够的有限公司(半)稳定条件

在[13]中，我们从对数正则阈值(lct)的角度研究了曲线B和C的奇异性(参见例[2，第8节])，并在(Y, F)对的lct和对的lct之间建立了一些精确的不等式。更准确地说，用(代表)表示。B的一个分量的最大多重数。F)，我们证明了以下几点:

引理4.1

([13，定理1.1和1.2])如果F是Y的任意(非多重)纤维，则对应的平面曲线B为

此外,

1. (i)

   如果F被简化了，那么B也被简化了

2. (2)

   如果(或者，等价地，F是非约简的)，则

3. (3)

   如果，则B是非约简的。

话4.2

请注意，数字lct(Y, F)由下表给出，具体取决于F的类型:

	类型的		类型的
1		1/2
5/6	2	1/6
3/4	3	1/4
2/3	4	1/3

我们还证明了:

引理4.3

[13，命题4.9]]曲线C的最坏节点为奇点。特别是……

相反，在[1]中，我们把铅笔的稳定性与:(i)铅笔上曲线的稳定性联系起来;(ii)对数正则阈值，其中为中的曲线;以及(iii)在基点上的生成器的多重性。

此外，Hacking[16]和Kim-Lee[17]观察到以下几点:

引理4.4

它是任意6次平面曲线，且(等)，则为半稳定(见图2)。稳定)，以保证SL的自然作用(3)。

特别地，我们看到可以尝试将上面的引理4.1,4.3和4.4与前面[1]中的一些结果结合起来，以获得指标2的Halphen铅笔的显式稳定性判据。这正是我们在本节所追求的。

具体来说，我们需要从[1]得到的结果如下:

引理4.5

([1，定理1.1])设铅笔包含一条曲线，这样。它是不稳定的。(不稳定)，则包含一条曲线，使得(参见。)．

引理4.6

([1，定理1.3])把铅笔插进去。如果我们能找到两条曲线，并且在这样的曲线中(p。)对于某个基点p，则是不稳定的。不稳定)。

引理4.7

([1，定理1.4和1.5])把铅笔插进去。

1. (i)

   它只有半稳定的。稳定)成员，则是半稳定(相对稳定)成员。稳定)。

2. (2)

   如果最多包含一条严格半稳定曲线(且其他曲线均为稳定曲线)，则为稳定曲线。

引理4.8

[1，定理1.6]]如果包含最多两条半稳定曲线，且(且中所有曲线都是稳定的)，则当且仅当存在一个单参数子群，使得和都是非稳定的，则是严格半稳定的。

以下4.4.1的标准

记住上面的结果，让我们用索引为2的铅笔，写成下面的形式。我们证明的第一个稳定性判据如下:

命题4.9

如果是非稳定的，则Y中含有非还原纤维。

证明

由于(引理4.3)，我们从引理4.5得出，如果铅笔是非稳定的，则包含一条曲线B，使得。根据引理4.1 (i)，这意味着相应的有理椭圆表面包含一个非约化纤维F。

当C是光滑的，B是半稳定的，我们也证明了:

命题4.10

如果C是光滑的，并且C中的所有曲线都是稳定的，除了(可能)一条曲线是半稳定的，那么C是稳定的。

证明

它直接由引理4.7和2C是稳定的这一事实得出[12]。

推论4.10.1

如果C是光滑的，F是或型的，对应的曲线是半稳定的，则是稳定的。

证明

根据[11]中的分类，我们知道Y的任何其他纤维都被还原了。根据引理4.1，我们也知道所有其他曲线都是简化的，并且对数正则阈值大于1/2。正如引理4.4中所观察到的，这意味着除了一条半稳定曲线外，所有的曲线都是稳定的。然后命题4.10得出了这个陈述。

推论4.10.2

如果C是光滑的，Y只包含一种类型的纤维F，那么它是稳定的。

证明

同样，从[11]的分类中我们知道Y的任何其他纤维都被减少了。由于曲线B是这样的(引理4.1)，根据引理4.4，它是半稳定的，并且我们可以像在推论4.10.1的证明中那样论证得出结论，除了(可能)一条曲线是半稳定的，所有的曲线都是稳定的。那么结果就从命题4.10中得出。

命题4.11

如果Y包含两种类型的纤维，则当且仅当存在单参数子群(且坐标在)使得类型的纤维对应的两条曲线相对于Y都是非稳定的，则Y是严格半稳定的。

证明

根据引理4.1，如果F是一类纤维，则对应的平面曲线B是，因此根据引理4.4，它是半稳定的。此外，通过[11]中的分类，我们知道C必须是光滑的，因此是稳定的[12];Y的所有其他纤维必须减少。特别是，最多包含两条半稳定曲线(其他曲线都是稳定的)，因此根据引理4.7总是半稳定的，由引理4.8得出结果。

推论4.11.1

如果Y包含两种类型的纤维，并且是严格半稳定的，则包含两条曲线和(不同于2C)，使得。而且，每条曲线都满足下列条件之一:

1. (i)

   它由一条双线和一个简化的四次线组成

2. (2)

   它被简化了，它有一个(唯一的)多重点，它(必然)是一个基点

3. (3)

   它被简化了，它有一个连续的三相点，它(必然)是一个基点。

证明

这两条曲线对应于两种类型的纤维。根据引理4.1，我们有。另一方面，如果是严格半稳定的，则命题4.11暗示两条曲线都是非稳定的，因此根据引理4.4。然后的描述出自[12，定理2.3]。这是唯一可能产生类型纤维的非稳定性材料。

结合命题4.9、推论4.10.2和4.10.1以及命题4.11，我们证明了:

命题4.12

假设C是光滑的，并且下列陈述之一成立

1. (i)

   Y的所有纤维都被还原;或

2. (2)

   Y只包含一个(非多个)类型的纤维F;或

3. (3)

   Y包含一根或型(非多重)光纤F，其对应的平面曲线B为半稳定;或

4. (iv)

   Y包含两种类型的纤维，并且不存在同时破坏两条相应曲线的单参数子群。

这样铅笔就稳定了。

在4.4节中，我们将进一步证明(命题4.28)，当C是光滑的，Y包含一个(非多重)光纤F型，对应的平面曲线B是不稳定的，那么也是稳定的。这样就完成了定理1.4中相反含义的证明。

现在我们分析C为奇异时的稳定性。根据[11]的分类，要么Y的所有纤维都减少了，要么Y只包含一种或类型的纤维。它不能包含两种类型的纤维(参见示例[11])。

鉴于命题4.9，我们将考虑包含未还原纤维F的情况，使得相应的曲线B是半稳定的。在这种情况下，铅笔将始终是半稳定的(引理4.7)，因为2C是半稳定的[12]，所有其他纤维必须减少-因此相应的曲线必须是稳定的引理4.5和4.4。

应用引理4.8，我们可以证明:

命题4.13

如果C是奇异的，并且Y恰好包含一个类型的纤维F，那么当且仅当存在一个单参数子群(和坐标)使得2C和都是非稳定的，则C是严格半稳定的。

命题4.14

如果C是奇异的，Y包含一个或类型的纤维F，曲线是半稳定的，那么当且仅当存在一个单参数子群(和坐标)使得2C和B相对于此都是不稳定的，则该曲线是严格半稳定的。

特别地，结合命题4.9、4.13和4.14，我们得到了定理1.5陈述的一部分:

命题4.15

假设C是单数，并且下列陈述之一成立

1. (i)

   Y的所有纤维都被还原;或

2. (i)

   Y包含一个(非多重)非还原光纤F，使得曲线是半稳定的，并且不存在同时使2C和B不稳定的单参数子群。

这样铅笔就稳定了。

现在，为了完成定理1.4和定理1.5的证明，我们需要得到成立的必要条件。特别地，我们需要证明，只要Y中含有或型的(非多重)纤维F，并且对应的曲线B是不稳定的，那么它就是不稳定的(命题4.24)。我们还需要更好地理解当F为类型纤维时的稳定性(第4.4节)。

正如已经提到的，对于这些最后的步骤，我们将利用第3节的结果和[13,7]节中的结构。

4.2 时的稳定性F属于类型

当F为类型时，根据[13，定理5.15]，曲线B只能通过以下平面曲线之一实现:

1. (i)

   三重曲线

2. (2)

   一个节点立方和一条拐点线，这条线的多重度为3

3. (3)

   两条三重线

4. (iv)

   一条曲线和一条切线，这条线的倍数为4

5. (v)

   一条具有5倍数的线和另一条线

根据[12]，如果B是三重二次曲线，则B是严格半稳定的，并且将永远是半稳定的(引理4.7):曲线2C根据[12]是半稳定的，并且所有其他纤维必须被约化——因此相应的曲线根据引理4.5和4.4必须是稳定的。

但有两种可能:C是光滑的，在这种情况下是稳定的(推论4.10.1);或者C是奇异的，那么C是严格半稳定的，当且仅当存在一个单参数子群(和座标)使得2C和B相对于C都是非稳定的(命题4.14)。

当B是(ii)， (iii)， (iv)或(v)中的曲线之一时，我们可以使用[13]中得到的显式结构来得出不稳定的结论。事实上，我们可以在中找到坐标，使得关于这些坐标的plencker坐标满足命题2.2的情形U(1)中的条件。

因此，当F为时，我们得到如下表征:

命题4.16

如果Y包含一种类型的纤维F，并且不是三重曲线，那么它是不稳定的。

证明

由于B不是三重二次曲线，有四种情况需要考虑:

1. (2)

   首先，假设B由一个节点立方和一条拐点线组成，这条线的多重度为3。然后[13，例7.58]，我们可以找到坐标，使曲线B有方程，C由。特别地，关于这些坐标的plicker坐标满足命题2.2的情形U(1)的条件，我们得出结论是不稳定的。注意，我们也可以像命题3.5 (v)中那样容易地检查。

2. (3)

   接下来，假设B由两条三重线组成。然后，可以证明其中一条线是C的拐点线，另一条线必须与三次数为2的三次线相切[13，例7.57]。特别地，我们可以找到B和C的坐标，其中。特别地，关于这些坐标的plencker坐标满足命题2.2的情形U(1)中的条件。而且，在这种情况下，我们又可以像命题3.5 (v)那样去检验它。

3. (iv)

   现在假设B由一条曲线和一条切线组成，这条线的倍数为4。那么[13，例7.59]与命题3.4中的(ii)一样。事实上，我们可以证明C一定与二次曲线相切。这条线)在具有6倍数的点上。两个)。特别地，我们可以找到坐标系使得B由多项式的零点给出而C由。因此，关于这些坐标的plicker坐标满足命题2.2的情形U(1)的条件，我们得出结论是不稳定的。

4. (v)

   最后，假设B由一条倍数为5的直线和另一条直线组成。根据命题3.3它是不稳定的。事实上，我们可以选择坐标，使B为曲线，C为某些的三次[13，例7.59]。注意，同样地，的pl cker坐标满足命题2.2中情形U(1)的消失条件。

这证明了定理1.6的正向含义。另一个含义将从下面的命题4.17开始，只要我们能够证明无论何时Y包含或类型的纤维F，那么它就不可能是不稳定的——这在第4.3节和4.4节(命题4.23和4.27)中得到了实现。

命题4.17

如果不稳定，则Y包含类型为或的纤维。

证明

这个证明与定理4.9的证明非常相似。由于我们由引理4.3知道，我们由引理4.5(通过取)得出，如果铅笔是不稳定的，则包含一条曲线B，使得。因此，引理4.1暗示Y包含类型为或的纤维。

4.3 时的稳定性F属于类型

现在我们考虑F是类型的情况。

根据[13，定理5.16]，曲线B只能由以下平面曲线之一实现:

1. (i)

   一条双线，一条立方线和另一条线

2. (2)

   一个双二次曲线和另一个二次曲线(半稳定)

3. (3)

   三次二次曲线(半稳定)

4. (iv)

   两条三重线

5. (v)

   一条三重线，一条圆锥线和一条直线

6. (vi)

   一条三重线，一条双线和另一条线

7. (七)

   一个三重线和一个立方

8. (八)

   一条曲线和一条直线，这条直线的倍数为4

9. (ix)

   一条具有4倍倍数的线和另外两条线

如果B是半稳定的，那么就像在类型纤维(三重圆锥)的情况下一样，我们可以根据引理4.7得出它总是半稳定的。同样，有两种可能性需要考虑:C是光滑的，在这种情况下是稳定的(推论4.10.1);或者C是单数，我们可以参考命题4.14。

当B不稳定时，我们可以再次使用在[13，第7节]中得到的显式结构来得出它是严格半稳定的结论。更准确地说，就像在类型纤维的情况下一样，我们可以首先表明:

引理4.18

(i):

当曲线B如(i)、(v)或(vi)所示时(直线处于一般位置)，则我们可以找到坐标，使得相对于这些坐标的plencker坐标满足命题2.3的情形NS(3)中的条件。

(二):

当B是(viii)或(ix)中的曲线之一时(p。(vii))我们可以在中找到坐标，使得相应的pl 克尔坐标满足命题2.3(参见)的情形NS(1)中的条件。提案2.3的案例NS(4)。

证明

如果B如(i)、(v)或(vi)中所示(行处于一般位置)，则必须分别如[13]中的例7.45、例7.51或例7.49所示。同样，如果曲线B如式(viii)或式(ix)所示(p。(vii))，则必须如实施例7.53或实施例7.54所示。例7.52)[13]中的。

那么，当B是(iv)或(vi)中的曲线之一(两条直线在某一点重合)时，我们可以应用以下引理得出在这些情况下B也是不稳定的:

引理4.19

如果包含一条曲线B和一个基点p，那么它是非稳定的。

证明

因为，结果遵循引理4.6应用于曲线和(和基点p)。

特别地，结合引理4.18和4.19，当F为类型时，我们得到如下表征:

命题4.20

如果Y包含不稳定类型的纤维F，则为不稳定纤维。

而且，我们可以证明下面的命题4.21和4.22，它们进一步暗示永远不可能是不稳定的。

命题4.21

如果Y包含类型为F的光纤，并且包含一条4倍线或3倍线，则是半稳定的。

证明

如果B包含一条多重性为4的直线并且是不稳定的，那么(和B)必然与命题3.4的情形之一相同。类似地，如果B包含一条三重线并且是不稳定的，那么(和B)必须与命题3.5的情况之一相同。如[13，第5节]所述，常规检查这些情况都不能产生具有类型纤维的有理椭圆曲面Y。

命题4.22

如果Y包含一根类型为F的纤维，由一条双线、一条三次线和另一条线组成，则Y是半稳定的。

证明

如果B由一条双线、一个立方体和另一条线组成，那么B必须是铅笔，如[13，例7.45]所示。更准确地说，B的形式是:

1. (i)

   D为节点三次，有节点;

2. (2)

   线为D的伸缩线，具有伸缩点;和

3. (3)

   这条线与D相交于另外两点，比如和。

而且，三次C是这样的，它穿过;它与D相切具有多重性的。因此，应用命题3.6，我们得出结论，必须是半稳定的。

现在，为了理解为什么曲线B和C必须如上所述，请注意，如果B由一条双线，一条三次线和另一条线组成，那么F的对偶图必须如下所示:

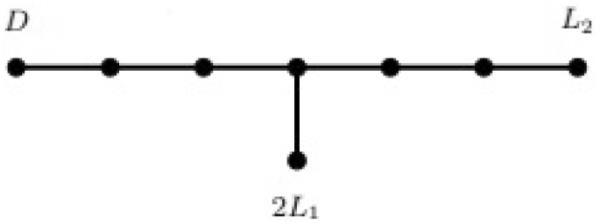
F的对偶图

其中我们标记了来自B的分量，未标记的黑色节点表示缺失的分量。参见[13，引理4.1]。

特别地，是在点上的放大，其中有一个点，并且无限靠近前一个点(阶为1)。这告诉我们C必须与D相切(阶为1)。具有多重性的。3)。

简单地说，我们这样证明了:

命题4.23

如果Y中含有一种类型的纤维F，那么它是半稳定的。

并且，结合命题4.16和4.20，我们还证明了:

命题4.24

如果Y中含有一根或类型的(非多重)光纤F，且对应的曲线B不稳定，则为不稳定。

4.4 时的稳定性F属于类型

最后，我们描述了当F为类型时的稳定性。我们证明要么是稳定的，要么C是奇异的，B是半稳定的，在这种情况下，我们可以参考命题4.14。

首先，我们观察到[13，定理5.17]，当F为类型时，则B必然是下列曲线之一:

1. (i)

   双二次曲线和二次曲线(半稳定)

2. (2)

   一条双线，一条圆锥线和两条线

3. (3)

   一条双线，一条立方，一条直线

4. (iv)

   一条双线和两条圆锥

5. (v)

   两条双线，两条线

6. (vi)

   两条双线和一条圆锥线

7. (七)

   双二次曲线和两条直线(半稳定)

8. (八)

   三次二次曲线(半稳定)

9. (xi)

   一条三重线，一条圆锥线和一条直线

10. (x)

    一条三重线，一条双线和另一条线

11. (xi)

    三条线和三条线

12. (十二)

    一个三重线和一个立方

此外，[13，节5]中的构造进一步暗示以下引理成立:

引理4.25

设一个指标2的铅笔，包含一条曲线B，其中L是一条直线，Q是一个四次(可能是可约的)。L和Q在任意点的交点多重不超过3。其中，B是半稳定的[12]。

证明

如[13，第5节]所述，检查L和Q在某点p的交集多重性为4，则B不能产生类型的纤维是常规的。注意p必须是的基点。

现在，如果B是半稳定的，那么就像在类型纤维(三次二次)的情况下一样，我们根据引理4.7得出它总是半稳定的。因此，根据引理4.25，还需要考虑B包含三条直线的情况。我们证明:

命题4.26

如果Y包含一种类型的纤维F，并且包含一条三重线，那么它是稳定的。

证明

如果它们是非稳定的，那么(和B)就会像命题3.7那样，通过取。例行的检查，如在命题3.7不能产生一个有理椭圆表面Y与类型的纤维(见例[13，第5节和第7节])。

我们特别在下面证明了命题4.27。

命题4.27

如果Y含有一种类型的纤维，那么它是半稳定的。

此外,

命题4.28

如果Y中含有非稳定型纤维，则C是奇异的，B是半稳定的。

证明

如果是非稳定的，那么从推论4.10.1可以得出C是奇异的或者B是不稳定的。Shah在[12，第2节]中对不稳定性的描述，以及对本节开头给出的曲线B的可能性的仔细分析，结合上述命题4.26和引理4.25，暗示B不可能是不稳定的。

这就是定理1.4、1.5和1.6的证明。结合命题4.12、4.24和4.28(参见。4.15, 4.24和4.28)证明定理1.4(参见。而定理1.6的证明则是由命题4.16、4.17、4.23和4.27组合而成。

目录

摘要
1 介绍
2 平面性铅笔的稳定性
3.不稳定和不稳定铅笔
4 指数二的半铅笔的稳定性
笔记
参考文献
致谢
作者信息
道德声明



搜索
导航

#####


下载原文档：https://link.springer.com/content/pdf/10.1007/s00229-022-01423-w.pdf